Histoire de cone (Jocobs ou din)

Bonsoir à tous.

Mécanicien d’opérette, je me suis lancé dans le changement du mandrin d'une petite perceuse d'établi. J'ai trouvé sur le forum comment démonter le mandrin, qui porte l'indication RJ33; J'en ai déduit qu'il s'agissait d'un mandrin pour cône Jacobs. Mais un doute m'étant venu, je viens de mesurer. Or si je suis les dimensions ci dessous :


Mes mesures sont incohérentes: 14,6 et 15,56 !

1) Mes mesures sont prises au pied à coulisse numérique de chez LID..(!)
2) Je ne suis pas sur de l'endroit sur cône où il faut prendre les mesures (

Vous auriez un conseil?

Bonjour

Le plus important n'est pas les diametres, mais la conicité.

Il faut calculer l'arctangente (ou tangente -1, sur certaines calculatrices) de (( grand diamètre - petit diamètre) / distance entre les diamètres. Ceci pour les deux cas. Si la conicité est identique ça doit se monter.

L'expérience semble indiquer que les deux ne sont pas équivalents et que si l'on monte un mandrin Jacobs sur un din (ou la converse), ça tombe.
Le calcul que vous proposez et qui permettrait  de connaitre" l'angle " du cône risque d'avoir un valeur théorique(on peut le faire avec les valeurs théoriques ci dessus).  Mais compte tenu du fait que ce sont les mesures "réelles" qui font problème, je ne comprends pas comment je vais déterminer à quelle type de cône j'ai à faire.

Pour le fun, l'angle pour un J33 est de 3.63 degrés contre 2.94 pour un B16

C'est pourtant simple.

Il suffit d'enfiler deux rondelles de diamètre intérieur différents sur le cône mâle et de mesurer la distance entre les deux cônes avec un pied a coulisse.

Autre solution : monter le cône entre pointes sur un tour et venir le palper avec un comparateur.

Troisième solution : emprunter un mandrin, peu importe qu'il soit Jacobs ou DIN passer le cône mâle au bleu, assembler les pièces et les faire tourner l'une dans l'autre pour voir si la portée est bonne.

Quatrième solution : prendre un autre cône mâle connu et le plaquet contre le premier. Si les deux axes sont parallèles, les deux cônes sont du même type, sinon, ils sont différents.

Mais, pourtant, pas encore assez, car convoquant un matériel qui n'est pas à ma disposition ( Même la première solution. Car la différence de conicité étant de 1.3 degrés, cela nécessite des mesures d'une précision qui excède celle de mon pied à coulisse, des "rondelles" et de leur positionnement)

On s'oriente plutôt vers l'achat de deux mandrins, non....?!

L’important est surtout l’angle ( ou la conicité) je te propose donc de mesurer deux diamètres et la longueur qui sépare ces deux diamètres
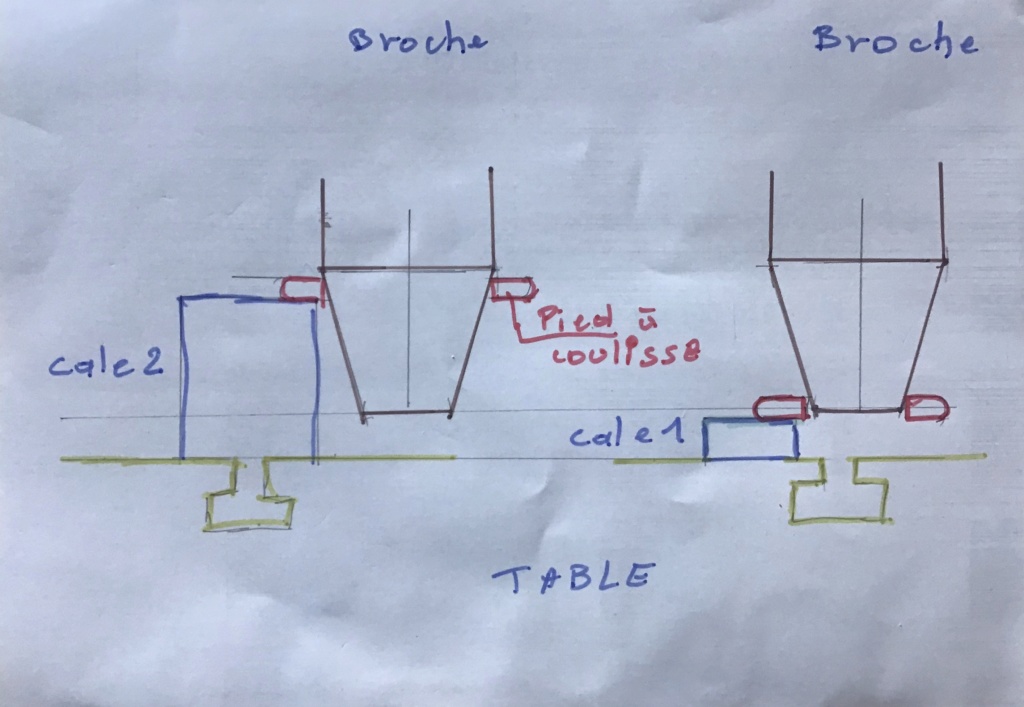
Pour ça on peut imaginer deux cales avec une différence de longueur connue (par exemple 20 et 30 )
Tu poses la cale de 30 sur la table  de ta perceuse
Tu pose ton pied à coulisse dessus
Tu descends la broche pour mesurer vers le gros diamètre
Tu bloque la broche
Tu mesures ton diamètre
Tu changes la cale ( hauteur 20 )
Tu remesures
Et tu calcules
Ça devrait ( Amon avis) fonctionner
Je rappelle à tout hasard les formules
(D–d)/L = conicité
Ou
(D–d)/(2xL) = Tangente

Ah ben mince ! Je viens de découvrir , est-ce que je me suis trompé? Que les conicités ne sont pas les mêmes entre les différents  cône Jacobs donc il faut faire le calcul en choisissant le cône le plus proche dans les dimensions

Il va me falloir un schéma! (je ne suis pas du tout mécanicien) D'autant que les cales, j'en ai pas. Tu n'as pas interverti les 2 formules?

Non je n’ai pas interverti les deux formules
La coniciré est le double de  la tangente
J’ai quand même réécrit  la formule pour qu’elle ne prête pas à confusion
Pour le schéma j’en fait un dès que possible  tu n’a pas de cales étalons c’est pas grave n’importe quel bout de ferraille avec deux faces parallèles peut convenir . Il faut simplement que leur hauteur soit compatible avec la hauteur de ton cône
Par exemple pour le J0 il faut une différence de hauteur entre 8 et 10 mm ; pour le J 33 il faut une différence de hauteur entre 18 et 24 mm

Je viens de voir que l’image n’est pas affichée en entier
Pour voir la totalité il faut cliquer sur l’ image

Super!

En fait,je me pose peut être des problèmes d'idiot, vu que le cône original est bien un J33.  Je viens de remesurer mais en prenant une valeur de L  qui permette une mesure "propre" et en me servant de la conicité, je retrouve bien les valeurs du tableau pour le J33! (Le cône est pris dans un roulement et à ce niveau, il y a une usure qui perturbait mon pied à coulisse)

C'est dur, la mécanique!

Merci à tous, en espérant que ces questions de profane serviront à aussi profane que moi.